The Ultimate Guide To Understanding The Area Of A Square
Understanding the area of a square is one of the most fundamental concepts in geometry, serving as a cornerstone for countless real-world applications. From designing a room to calculating land plots, grasping how to measure the space a square occupies is an indispensable skill. This guide will delve deep into everything you need to know about this essential mathematical concept, ensuring you gain a clear and practical understanding.
Whether you're a student grappling with geometry homework, a DIY enthusiast planning a home improvement project, or simply curious about the world around you, mastering the calculation of a square's area is incredibly useful. We'll explore the core formulas, walk through practical examples, discuss its relevance in three-dimensional shapes, and even touch upon more advanced topics like scaling and inscribed squares. By the end of this article, you'll not only know how to calculate the area of a square but also truly appreciate its significance.
Table of Contents
- What Exactly is the Area of a Square?
- The Fundamental Formula for Area of a Square
- Area vs. Perimeter: Understanding the Difference
- Finding the Side Length When You Know the Area
- The Area of a Square in 3D Geometry
- Advanced Concepts: Scaling and Inscribed Squares
- Why Understanding the Area of a Square Matters
- Common Mistakes and Tips for Accuracy
What Exactly is the Area of a Square?
At its core, the concept of "area" refers to the amount of two-dimensional space a flat figure occupies. Think of it as the amount of paint you would need to cover a surface, or the number of unit squares that could fit inside a given shape. For instance, when we talk about vast geographical expanses, like the area of Brazil being 3,287,957 square miles or 8,515,770 square kilometers, we are quantifying the total landmass it takes up. This principle applies universally, whether to a country or a small square on your desk. A square is a unique and fundamental geometric shape, characterized by four equal sides and four right (90-degree) angles. It's essentially a special type of rectangle where all sides are of the same length. This particular characteristic simplifies its area calculation significantly. Unlike a general rectangle where you might have different lengths for its sides, in the case of a square, the length and width are the same value. This means that to find the area, you simply multiply the length of one of its sides by itself. This inherent symmetry makes the area of a square one of the most straightforward geometric measurements to master.The Fundamental Formula for Area of a Square
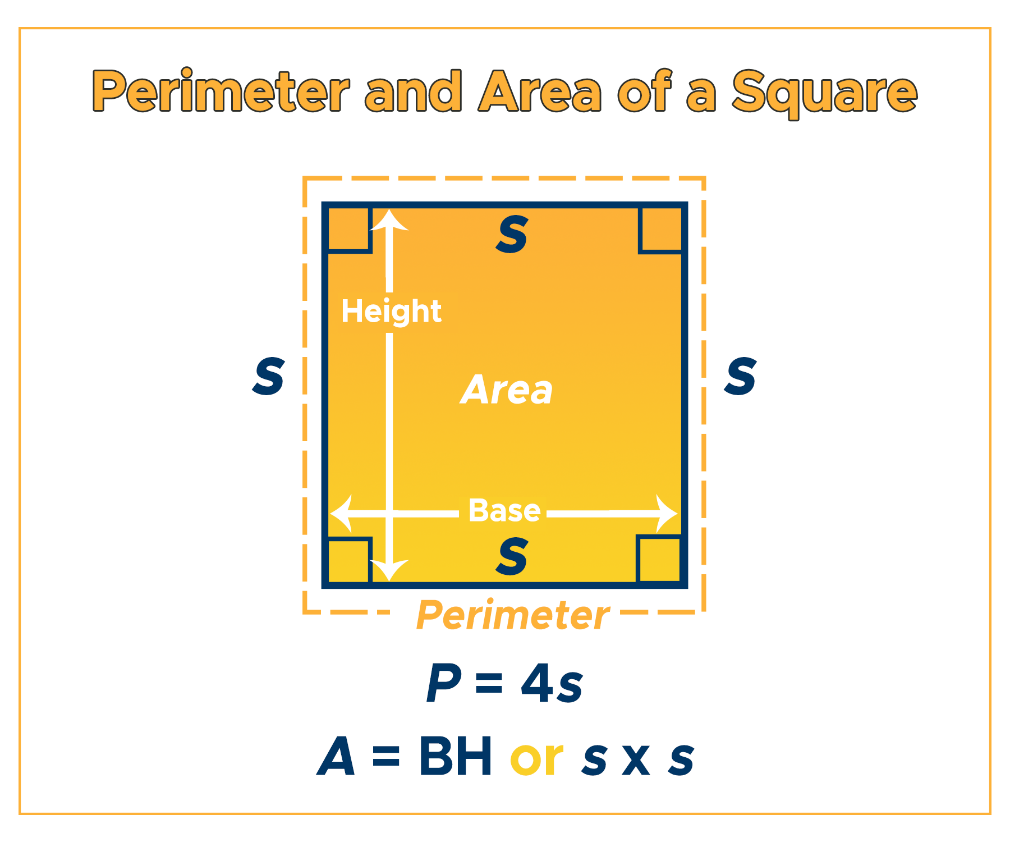
The beauty of calculating the area of a square lies in its simplicity. The formula is elegantly straightforward and only requires one piece of information: the length of its side. Remember, the formula for finding the area of a square is expressed as `a = s²`, where 'a' stands for area and 's' represents the length of one side. This can also be thought of as "side times side." More formally, if we denote the side length as `ℓ`, the formula becomes `{eq}a = \ell \times \ell = \ell^2 {/eq}`. This mathematical notation simply reinforces the idea that you are multiplying the side length by itself. The reason for this `s²` (or `ℓ²`) is precisely because, as mentioned, a square's length and width are identical. Imagine a grid of small unit squares. If a square has a side length of 3 units, you can fit 3 rows of 3 unit squares inside it, totaling 9 unit squares. This visual representation directly translates to 3 multiplied by 3, or 3². This principle holds true for any square, regardless of its size.Practical Example: Calculating Area from Side Length
Let's put the formula into practice with a couple of clear examples. Suppose you have a square tile, and the sides of this particular square are 5 inches. To find its area, you simply plug that value into the formula: `a = s²` `a = 5²` `a = 5 × 5` `a = 25 in²` So, the area of this square tile is 25 square inches. This means that 25 individual 1-inch by 1-inch squares could perfectly cover its surface. Consider another scenario: a small garden patch shaped like a square, with each side measuring 5 meters. Following the same principle, the area of a square with sides of 5 meters is equal to 25 square meters. This indicates the amount of land space the garden occupies. These simple formulas and their explanations are given below, showing just how easy it is to calculate the area and perimeter of a square when its side length is known.Area vs. Perimeter: Understanding the Difference
While often discussed together, the area and perimeter of a square represent distinct measurements and serve different purposes. It's crucial not to confuse them. As we've established, the area of a square is `a = s²`, or side times side. It quantifies the two-dimensional space enclosed within the boundaries of the square. Think of it as the surface you'd paint or the carpet you'd lay down. The units for area are always "square units" (e.g., square inches, square meters, square feet). On the other hand, the perimeter of a square is `p = 4s`, or 4 times s. The perimeter measures the total length of the boundary or outline of the square. Imagine walking around the edge of the square; the distance you cover would be its perimeter. The units for perimeter are linear units (e.g., inches, meters, feet), just like measuring a length. For our 5-inch square tile example: * Area = 25 in² (the space it covers) * Perimeter = 4 × 5 = 20 inches (the length of its edges) Understanding this distinction is vital for accurate calculations in various applications, from fencing a yard (perimeter) to laying turf (area).Finding the Side Length When You Know the Area
Sometimes, you might know the area of a square but need to determine the length of its side. This is the inverse operation of calculating the area. Since the area formula is `a = s²`, to find 's' when 'a' is known, you need to perform the opposite operation of squaring, which is taking the square root. So, if `a = s²`, then `s = √a`. To find the length of one side by plugging the area value into the formula and then taking the square root, you can easily deduce the side length. For example, if you know a square room has an area of 49 square feet, you can find the side length: `s = √49` `s = 7 feet` This means each side of the square room is 7 feet long. This skill is particularly useful in design and construction, where you might have a specific area requirement and need to determine the dimensions.The Area of a Square in 3D Geometry
The concept of the area of a square isn't confined to flat, two-dimensional shapes. It plays a crucial role in understanding and calculating properties of three-dimensional objects, especially those with square bases or faces. Consider a pyramid, for instance. The base of the pyramid is often a square. If each side of the square base, 's', is 5 cm, then its area is `s × s` or `5 × 5 = 25 cm²`. This base area is often denoted as 'b' in formulas for the volume or surface area of pyramids. Understanding the area of this square base is the first step in calculating the pyramid's overall volume or surface area.Cubes and Prisms: Square Bases in Action
Cubes and square prisms are prime examples where the area of a square is fundamental. A cube, by definition, is a three-dimensional solid object bounded by six square faces. Each face is a perfect square. A square prism is a prism with a square base. When calculating the surface area of such objects, the area of the square base (or face) becomes a critical component. For a general prism, the formula for surface area is `surface area = 2b + ph`, where `b` represents the area of the base, `p` is the perimeter of the base, and `h` is the height of the prism. If the base is a square, then `b` would be `s²` (the area of the square base), and `p` would be `4s` (the perimeter of the square base). For example, if you have a square prism with a base side length of 6 cm and a height of 10 cm: * Area of the square base (b) = 6² = 36 cm² * Perimeter of the square base (p) = 4 × 6 = 24 cm * Surface area = 2(36) + (24)(10) = 72 + 240 = 312 cm² This demonstrates how the fundamental understanding of the area of a square directly feeds into more complex 3D calculations, such as the surface area of a tube (which might have a circular base, but the principle of base area applies similarly) or a pipe. The principles are universal, adapting to the specific shape of the base.Advanced Concepts: Scaling and Inscribed Squares
Beyond basic calculations, the area of a square plays a role in more complex geometric transformations and relationships.Scaling Areas of Similar Squares
When you scale a figure, you're essentially stretching or shrinking it in all directions by a certain factor, known as the scale factor. This process, called dilation, affects the area in a predictable way. The ratio of the areas of two similar figures (like two squares of different sizes) is equal to the square of the ratio of their corresponding sides. For example, if you have a square with a side length of 2 units (Area = 4 units²) and you dilate it by a scale factor of 3, the new square will have a side length of 2 × 3 = 6 units. Its new area will be 6² = 36 units². Let's check the ratio: Ratio of sides = New side / Original side = 6 / 2 = 3 Ratio of areas = New area / Original area = 36 / 4 = 9 Notice that 9 is 3², confirming that the ratio of the areas is the square of the ratio of the corresponding sides. This principle is incredibly useful in architecture, engineering, and design when scaling models or blueprints.Inscribing a Square within a Circle
Another intriguing application involves inscribing a square within a circle. This means drawing a square inside a circle such that all four vertices of the square touch the circle's circumference. If the diameter or the radius of the circle is known, you can find the length of the diagonal of the square using the fact that the diameter of the circle is equal to the diagonal of the inscribed square. Let's say a circle has a radius of 8 units. Its diameter would be 16 units. This 16-unit diameter is also the diagonal of the inscribed square. In a square, the diagonal (d) is related to the side (s) by the Pythagorean theorem: `d² = s² + s²`, which simplifies to `d² = 2s²`, or `d = s√2`. So, if the diagonal `d = 16`, then `16 = s√2`. Solving for `s`: `s = 16 / √2 = 16√2 / 2 = 8√2`. Once you have the side length `s = 8√2`, you can find the area of the inscribed square: `Area = s² = (8√2)² = 8² × (√2)² = 64 × 2 = 128 square units`. For comparison, the area of the circle itself is found by multiplying 3.14 (or pi) times the square of the radius (8), so the area of the circle is approximately `3.14 × 8² = 3.14 × 64 = 200.96 ft²`. This shows how the area of the inscribed square relates to the area of the circle that contains it, a concept crucial in fields like manufacturing and material optimization.Why Understanding the Area of a Square Matters
Beyond the classroom, the ability to calculate the area of a square is a practical skill with wide-ranging applications that can significantly impact your daily life and financial decisions. This makes it a YMYL (Your Money or Your Life) relevant topic in many contexts. * **Real Estate and Property:** When buying or selling land or a house, understanding square footage (or square meters) is paramount. The value of a property is often directly tied to its area. Miscalculating the area of a square plot of land could lead to significant financial loss or gain. This knowledge helps you verify property listings, plan for renovations, or even assess potential property taxes. * **Home Improvement and Construction:** Planning to tile a bathroom, lay new flooring, paint a wall, or build a deck? All these tasks require accurate area calculations to determine the amount of materials needed. Overestimating leads to wasted money on excess materials, while underestimating leads to delays and additional trips to the store. For instance, calculating the area of a rectangle (or a square, as a special type of rectangle) is fundamental for purchasing the correct amount of carpet or paint. * **Design and Arts:** From graphic design to interior decorating, understanding how space is occupied and proportioned is key. Designing a square logo, arranging furniture in a square room, or even quilting requires a precise grasp of area to achieve desired aesthetics and functionality. * **Manufacturing and Engineering:** In engineering, calculating the cross-sectional area of components, often square, is crucial for stress analysis, material strength, and overall structural integrity. In manufacturing, determining the area of materials needed for production directly impacts cost and efficiency. * **Gardening and Landscaping:** Planning a square garden bed or calculating how much topsoil or fertilizer is needed for a square patch of lawn relies heavily on area calculations. * **Gaming and Software Development:** Many game environments and software interfaces are built upon grid systems, where understanding the area of square "cells" is fundamental for collision detection, rendering, and resource management. In essence, the area of a square is not just a theoretical concept; it's a practical tool that empowers you to make informed decisions, manage resources efficiently, and accurately plan for various real-world scenarios.Common Mistakes and Tips for Accuracy
While calculating the area of a square seems simple, certain common errors can lead to inaccuracies. Being aware of these pitfalls can help you ensure precision in your calculations. 1. **Confusing Area with Perimeter:** This is perhaps the most frequent mistake. Remember, area is `s²` (square units), and perimeter is `4s` (linear units). Always double-check which measurement you need for a given problem or task. 2. **Incorrect Units:** Always pay attention to the units given in the problem and ensure your final answer is expressed in the correct square units (e.g., in², m², ft²). If side lengths are in different units, convert them to a consistent unit before calculating the area. 3. **Calculation Errors:** Even simple multiplication can go wrong. Always double-check your arithmetic, especially when dealing with larger numbers or decimals. 4. **Misidentifying the Shape:** Ensure the figure you're working with is indeed a square. If it's a rectangle with unequal sides, you'll need to use the formula for a rectangle (length × width). **Tips for Accuracy:** * **Visualize:** Imagine the square and the space it covers. This can help solidify your understanding. * **Write Down the Formula:** Always start by writing `a = s²` before plugging in numbers. This reinforces the process. * **Label Units:** Consistently label your measurements with units throughout your calculation and in your final answer. * **Use Examples:** Practice with various examples, like the 5-inch or 5-meter squares, to build confidence. * **Check Your Work:** If possible, re-calculate using a different method or a calculator to verify your answer. By being mindful of these points, you can significantly improve the accuracy and reliability of your area calculations, ensuring your projects and decisions are based on solid mathematical foundations.Conclusion
The area of a square is far more than just a simple geometric formula; it's a foundational concept with immense practical utility across countless fields. From its straightforward calculation using `a = s²` to its application in three-dimensional shapes, scaling, and even complex inscribed figures, understanding this concept empowers you with a valuable tool for problem-solving in the real world. We've explored how the area quantifies the space a square occupies, differentiated it from perimeter, and demonstrated its relevance in everything from home renovation to large-scale engineering. Mastering the area of a square is an essential step in building a strong mathematical foundation, enabling you to make more informed decisions in your personal and professional life. We hope this comprehensive guide has illuminated the simplicity and power of this fundamental geometric measurement. Do you have a square-related project you're working on, or perhaps a tricky area problem you've encountered? Share your thoughts and questions in the comments below! Your insights help our community grow. If you found this article helpful, consider sharing it with others who might benefit, and explore our other guides on related geometric concepts to further expand your knowledge.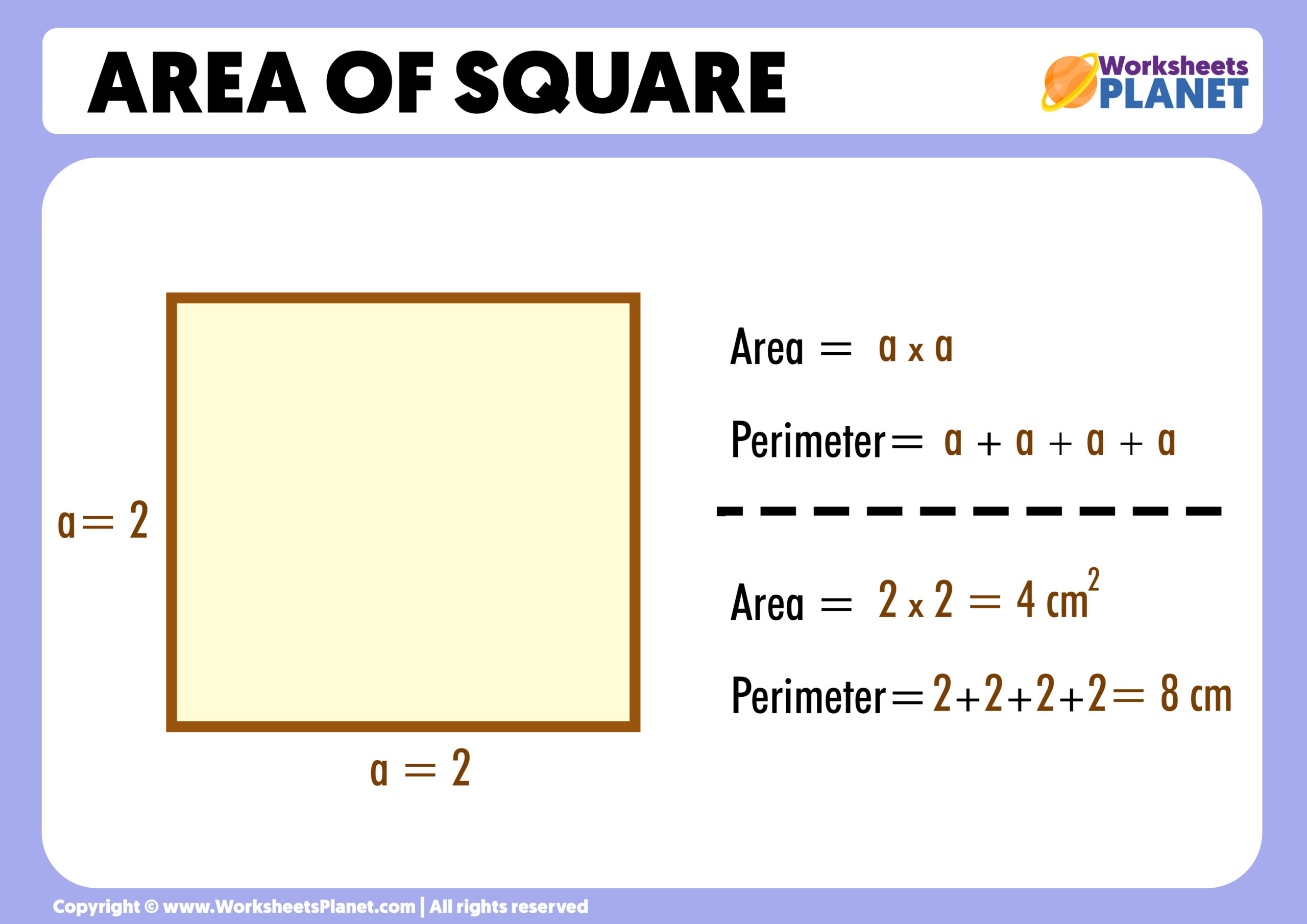
Area of a Square

Area of Square Formula | ChiliMath
Area of a Square: Formula & Examples - Curvebreakers